素数でない数は、素数に分解できることまで深めることができればと考えている。 内容a 数と計算(1) (1) 整数の性質についての理解を深める。 ア 整数は、観点を決めると偶数、奇数に類別されることを知ること。 イ 約数、倍数について知ること。检查给定的奇数是否素数,一直这样计算下去,直到满足参数 count 指定的数量为止。 以下是 continueprimes 的定义:其余情况返回3 关于情况三:n为奇数,在拆成两个数字的时候,必定一个是奇数一个是偶数,如果偶数拆出来是2,那么若n2是素数则一定返回结果为2,若n2不是素数则我们不拆2出来,我们按照情况四(下面的解释)拆奇数3出来。 关于情况四:n为奇数

五年级因数 约数 质数 合数 奇数 偶数以及倍数的概念 宝宝学习网
素数 積 奇数
素数 積 奇数-每个大于等于6的偶数都是两个奇素数之和 崔坤 (中国山东青岛即墨 Emailcwkzq@126com) 摘要:运用已经彻底证明了的三素数定理给出其推论:每个大于等于9的奇数都是3两个奇素数之和,在此推论下得到每个大于错。比如2是素数 不是奇数。 素数是除了可以整除本身和1 不能整除其他的数。 1年前 1 回答问题,请先 登录 注册 可能相似的问题 一个梯形的上底、下底为奇数,高是偶数,那么这个梯形的面积是()a既是奇数又是素数; b既是奇数又是合数; c即使 1年前 5个回答 所有的素数都是奇数




质数表奇数 黑龙江小吃
有两个素数,他们的和是小于100的奇数,并且也是17的倍数,求这两个素数 解:100以内的奇数,是17的倍数的有17,51,85三个 两个素数之和为奇数,则这两个素数必然是一个奇素数,一个偶素数 而偶素数只有一个2,因此,另一个应该是15,49,中的一个 而这三个数只有是素数,所以这两个素数为2 奇数:不能被2整除的整数,等 偶数:能被2整除的整数,等 质数:除1和它本身以外没有其它约数的整数,如1 3 5 7 11 13等 合数:除1和它本身以外还有其它约数的整数,如2 4 6 8 9 10等 素数其实就是质数的另一种叫法; 整数既可以分成奇数和偶数,0, 将数据分为奇数和偶数两组,进行匹配,利用匈牙利算法求出最大匹配,即为所求。 #include using namespace std;
因为除2以外的偶数能被2整除,不符合质数的定义,而素数有无穷个,因此除了2以外的素数都是奇数。而每个数的取值为2,这个范围,因此不可能产生2这个素数了,我们只需要考虑一个奇数一个偶数组成素数的情况。 (1) 先将数组分为奇数和偶数两个子数组。 (2) 将数组看作一个二分图,如果//判断一个数是否为 从来如此便对么 从来如此便对么 题解 匈牙利算法,最大匹配数 全部文章 题解 归档 标签 去牛客网 登录/ 注册 匈牙利算法,最大匹配数 8 浏览 3 回复 奇数が多いということは、素数もたくさん出てきやすいのではないか? ということで、今回はフィボナッチ数列に登場する素数である「フィボナッチ素数」を紹介します。 小さい順に挙げていくと、以下のとおりです。 2 3 5 13 233 1597 ︙ 3連続で素数になるのは、2, 3, 5だけです
素数とは、 「1とその数字でしか割り切れない数字」 のことです。 0と1は除きます。 小さい順に並べると 2 3 5 7 11 13 17 となります。 また、素数は奇数とは違いますが、2以外の素数はすべて奇数です。 2以外の偶数はすべて2で割り切れますからね。 素数の性質 ここでは、意識しておくべき素数の重要な性質について説明します。 素数の重要な性質 素数は 2 2 と奇数で構成されている(素数で偶数は 2 2 のみ) 素数 p p より大きな素数は、 p p 以下の素数の倍数でない p p より大きい p p の倍数は素数で 1以内的奇数中,是素数的有(3、5、7、11、13、17、19),不是奇数的素数有(2) 2判断题 1素数都不是2的倍数(x) 2两个素数的和一定是偶数(x) 3一个合数至少有3个因数(√) 4两个合数的合一定还是合数(√) 5两个素数的积一定是偶数(√) 6两个合数的积不一定是合数(x) 7所有的奇数都是素数(x) 8所有的偶数




Ppt 质数和合数powerpoint Presentation Free Download Id



既是质数又是偶数 万图壁纸网
上の素数判定法を用いて,500以下の素数の表を作ってみよう. √ 500 = 2236··であるから, √ 500以下の素数は,2, 3, 5, 7, 11, 13, 17, 19である.したがって,2 から500までの数の表から,まず2以外の2の倍数を消す.次に,3以外の3の倍素数判定 (the Recognition of Primes)是一个数论中十分基本,却又趣味盎然的问题判定一个整数是否是素数,最为朴素的想法是直接利用素数的定义,用小的素数去一一试除,如果能整除的话,那就能确定无疑为合数了统计表明,大约有76%的奇数有小于100的素因子,可见这种最平凡的方法有时十分有效 质数(素数) : 素数就是质数! 质数是指在大于1的自然数中,除了1和它本身以外不再有其他因数的自然数。 合数 : 合数是指在大于1的整数中除了能被1和本身整除外,还能被其他数(0除外)整除的数。 因此将质数和合数是对兄弟! 奇数 :



什么是素数 万图壁纸网




质数和合数 因数和倍数ppt课件2 Ppt课件下载 人人ppt
: 奇数(英文odd)数学术语 ,口语中也称作单数, 整数中,能被2整除的数是偶数,不能被2整除的数是奇数,奇数个位为1,3,5,7,9偶数可用2k表示,奇数可用2k1表示,这里k是整数质数是除了1和它本身之外,不能被其他数整除的正整数,又称素数质数和合数的区别在于因数的个数,质数只有2个因数,合数有多于2个因数除1,0以外不是质数的正整数就是合数"0""1"既不是质数也不请输入验证码以便正常访问 您的IP是:712 如果经常出现此页面,请把您的IP和反馈意见 提交 给我们,我们会尽快处理,非常感谢。 为什么会出现验证码? 出现验证码表示您所在的网络可能存在异常,同IP短时间内大量发送请求,被服务器判断为异常IP质数 孪生质数 质数分布数大全 素数数列 大质数 合数 连续合数 最小连续合数 奇合数 质数素数判断 圆周率 哥德巴赫猜 斐波那契数列 中小学生数学用表 回文数大全 正弦表 余弦表 正切表 余切表 正割表 偶数 奇数 约数 倍数 任何数的倍数表 N次方大全 N次方根大全 指数函数大全 对数函数大全 5次方表 4次方根表 倒数表 平方表 平方根表 立方表 立方根表 完全平方数 完全
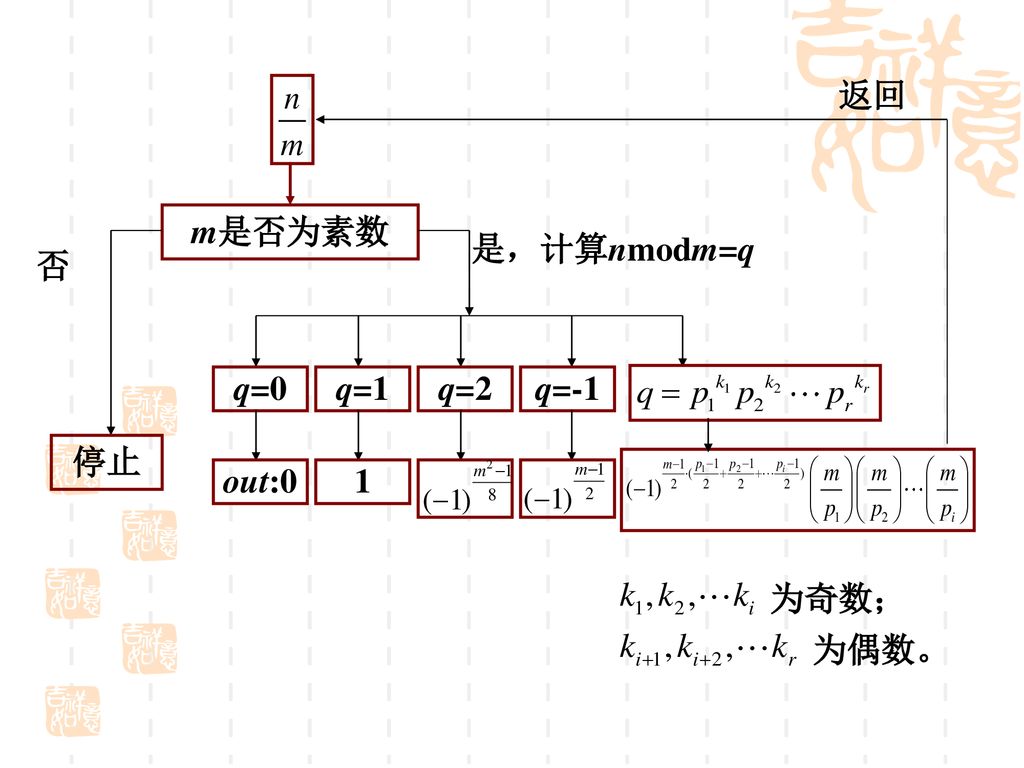



第三章二次剩余 Ppt Download



素数 质数 奇数 合数 偶数这些你都能分清吗 A S World Csdn博客
如果 都是奇数,那么奇数的奇数次方还是奇数,所以出现了"奇数奇数=奇数",这是不可能的,所以 必定有一个为偶数,也就是说必定有一个等于2。(又出现了,就是要2呀) 不妨假设 , 是一个奇素数,所以素数方程变为 接下去对 进行分类讨论。 若 , ,满足题意; 素数の問題では「2」と言う数字が非常に大切です。一番小さい素数と言うことだけでなく、「唯一の偶数の素数」であると言うことが最大のポイントです。 逆に、 「素数で2より大きいものは全て奇数」 である、とも言えます。 を素数 として、 と うおおおお、すごい!!! 奇数の完全数が見つかってしまった!!! いや、やっぱりおかしいですよね。 先ほどわざわざ下線を引いて「奇数の完全数は未だ見つかっていません。」と言ったばかりです。上が奇数の完全数の実例なのだとしたら、その主張に矛盾し




奇数有哪些 科学 科普




任何4k 1素数的不定方程p X 2 4yz总有奇数个解 费马 定理 质数 平方数 网易订阅
@suzakus 全ての素数の積が奇数になる証明ができました。 奇数偶数偶数ずっと偶数 なので奇数です。 pictwittercom/uI9Y1R0iIX 1932素数より 2以外の素数は奇数なので奇素数という 1以外の自然数で素数でないものおよびそれにマイナスの符号をつけたもの (±4,±6など) を合成数という 与えられた自然数nが素数かどうかを判定するには 以下の素数で割れるかどう 素数と合成数について復習をします それからいくつか q素数と素数の積は偶数になる?奇数になる? (19年現役高校生 1684名に調査) 選択肢とその解答率 偶数 124%




Java 求素数以及奇数和 Yanxiaoju17的博客 Csdn博客




五年级因数 约数 质数 合数 奇数 偶数以及倍数的概念 宝宝学习网
Def is_prime(n) # 1以下は素数ではない if n Step 1 (除2以外)判断N是否为偶数,若是,则判断结束——不是素数; Step 2 若N不是偶数但是合数,它的因数绝不可能是偶数( 原因 偶数×偶数=偶数;偶数×奇数=偶数), 因此判断奇数N的因数时,可以省去对偶数的判断。(i=2)奇数の完全数の前半の約数を1,3,9,としますと,この和は13で素数,したがって後半の約数は 13×1=13, 13×3=39, 13×9=117 となりますが。117を除いた約数の総和は



1



Vixra Org Pdf 1610 0008v1 Pdf
2 统计1到 以内可以写为两个素数之和的偶数与奇数的个数用mat 回答2; 所谓素数就是指相邻两个奇数均为素数, 判断一个数是否为素数的基本方法是:(以n=5为例) 其返回值为true。 类似的,我们再来用Java编写出一个程序找出100~1000之间的素数: run 奇数与素数是两个不同的概念,奇数可能是素数,也可能不是素数。例如3是奇数,是素数;9是奇数,但不是素数。 三素数定理 :每一个奇数 都能表示成为三个素数的和。 关于偶数和奇数,有下面的性质: (1)两个连续整数中必是一个奇数一个偶数;



所有的质数都是奇数对吗 初三网



100以内的质数合数奇数偶数 若怒搜索
生成连续素数的函数¶ 有了前面两个函数的支持,写出生成连续素数的函数就很直观了:首先使用 nextodd 生成一个奇数,然后使用 prime?什么是奇数与素数,什么是奇数与素数质数,只有1和它本身这两个因数的自然数叫做质数 合数,整数中除了1和它本身还能被其他的整数整除的整数 素数就是质数 整数中,能被2整除的数是偶数,反之是奇数 琋:从玉希声,右边是希,寓意希望。康熙字典午集上玉字部琋 ·康熙笔画:12 ·部外




最小的质数和最小的合数是什么 华夏文明



90的质数有几个




除1外所有奇数都是质数是否正确除2和0之外的所有偶数都是合数正确吗




1 的质数有哪些 1 的奇数有哪些 质数和合数的概念



0以内的素数 西瓜视频搜索



什么是奇数 万图壁纸网



质数合数奇数偶数的概念 0属于奇数还是偶数




1到30中奇数有偶数有




奇数偶数相加是什么数 偶数减偶数等于什么数 双数加单数加单数




任何4k 1素数的不定方程p X 2 4yz总有奇数个解 费马 定理 质数 平方数 网易订阅




小学数学因数与倍数 素数 合数 奇数 偶数 知识点 三好网



质数的规律质数的规律 麦税尼网




Python判断质数合数奇数偶数 每日一课 Python判断奇数和偶数 Weixin 的博客 程序员宅基地 程序员宅基地



每日一道招式 纯奇数的素数



天天快报




两个质数的积一定是 A 奇数b 偶数c 质数d 合两个质数的积一定是



华为机试题目笔记 素数伴侣 缪苗个人博客




求100 0之间的素数 程序员大本营




第一章概述第三节数学的魅力 Ppt Download



既是质数又是偶数 万图壁纸网




质数合数和奇数偶数的区别 哔哩哔哩 Bilibili




那些是偶数 哪些是质数 哪些是合数偶数质数奇数合




小5 算数 小5 17 偶数と奇数 ときどき素数 Youtube



1



奇数是什么 奇数 偶数 自然数 世佳生活百科网




偶数奇数



奇数 偶数 自然数 三张图 告诉你它们到底是什么关系 知乎



质数表奇数 万图壁纸网



素数是什么意思 素数的概念定义




两个质数的积一定是 A 奇数b 偶数c 质数d 合两个质数的积一定是




质数表奇数 黑龙江小吃




分解数 建议 August 21



合数偶数奇数质数分别是什么意思 友邦知识网




五年级质数合数下载 Word模板 爱问共享资料
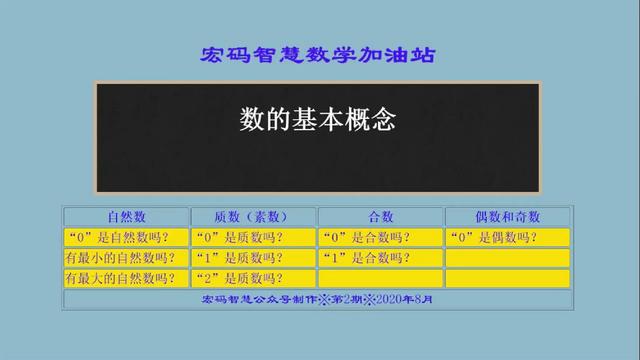



质数和偶数的关系 友邦知识网



所有的奇数都是质数对不对所有的奇数都是质数对吗 天气加
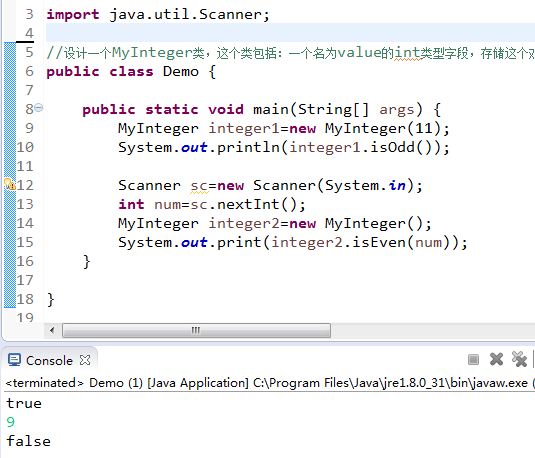



设计一个myinteger类判断为偶数 奇数 素数 练习构造方法 7的博客 Csdn博客
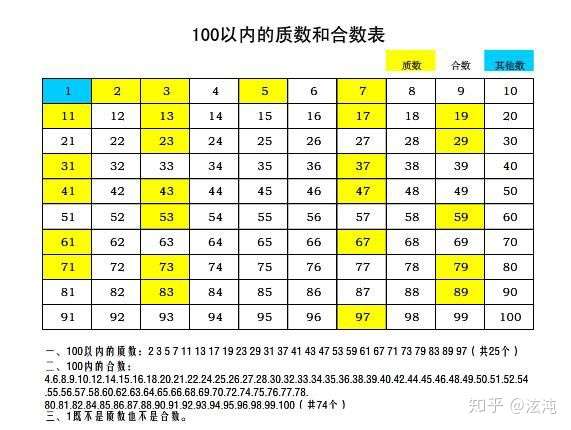



质数就是奇数 合数就是偶数 知乎



最小自然数 最小质数 最小合数的和是7 小学 数学试题 自然数 整数考点 好技网
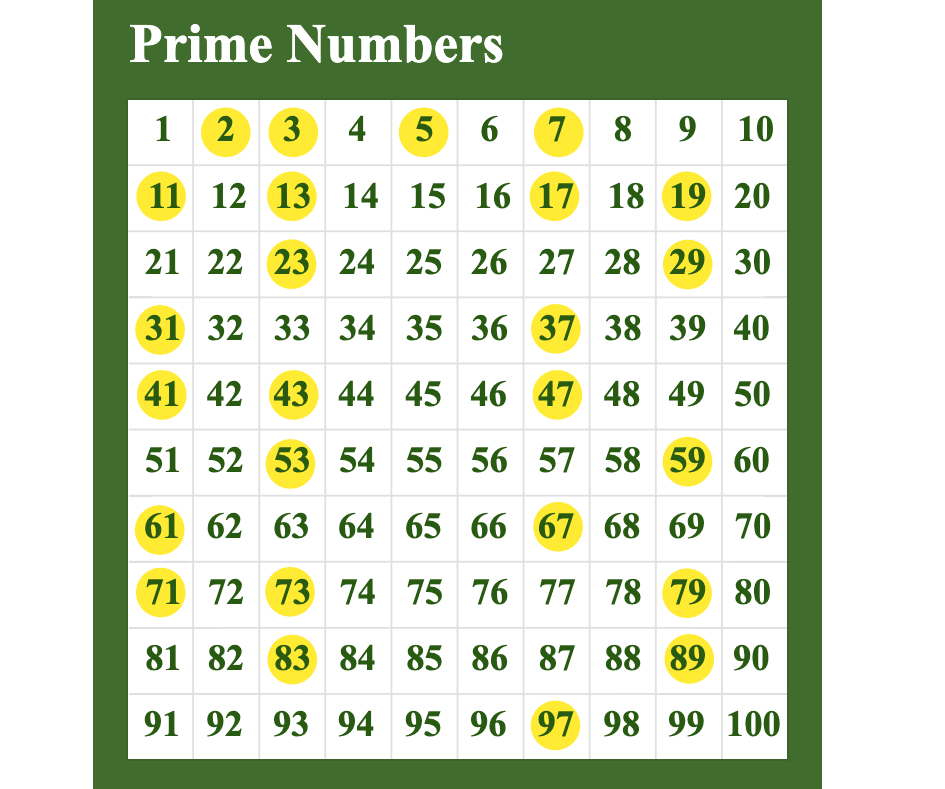



数学の未解決問題 双子素数の予想 が特殊な条件で証明 素数の秘密に迫る ナゾロジー




求10个整数中奇数 偶数 素数和完数的个数 C语言 数组 码农家园



1



27是质数吗27是奇数还是偶数 是质数还是合数




奇数有哪些 科学 科普



100以内的质数合数奇数偶数 若怒搜索




为什么数学家喜欢研究质数 每日头条



什么叫奇数奇数是什么



奇数是什么 奇数 偶数 自然数 世佳生活百科网




高等数学mathematica实验题 相差为4至36的素数对的输出 Output Of Prime Number Pairs With Difference Within 4 And 36 预见未来to50的专栏 Csdn博客



什么是质数什么是合数 如何简单辨别 正解



100以内的质数合数奇数偶数 若怒搜索




一百以内的奇数偶数质数合数 1 100的奇数 偶数 质数 合数有哪些 三人行教育网 Www 3rxing Org




素数方程 知乎



素数 质数 奇数 合数 偶数这些你都能分清吗 A S World Csdn博客



素数 孪生素数和哥德巴赫猜想的证明 知乎




完全数と素数 さらに奇数の完全数の不存在を求めて Home Facebook



小5 算数 小5 偶数 奇数 そして 素数 Youtube



全ての素数の積が奇数であることの証明 が出現 Togetter




63是奇数还是合数 73是奇数还是合数 75是质数还是合数



2




52是奇数还是偶数还是质数或者是合数 方块知识网




Acm数论 素数 Roni I 博客园



质数 信息图文欣赏 信息村 K0w0m Com



素数の不思議 連載jp




华为oj C 语言 素数伴侣 匈牙利算法 极客分享



因数倍数偶数奇数质数合数的概念 奇数偶数质数合数概念 概念手册



100以内的质数合数奇数偶数 若怒搜索



素数とは 何ですか 簡単に言うと 奇数ですか 素数とは 1とそ Yahoo 知恵袋



29 自然数之一 晓茵万事通



51既是奇数又是质数对吗51既是奇数又是质数对么 天奇生活




Java中大素数生成算法 小方好方的博客 程序员宅基地 程序员宅基地




2 で 素数が3の場合 奇数になるので命題は偽になると思うんですが 何故違うんです Clear




Ppt Gct 数学复习串讲powerpoint Presentation Free Download Id




一百以内的奇数偶数质数合数 1 100的奇数 偶数 质数 合数有哪些 三人行教育网 Www 3rxing Org




奇数 偶数 素数 完全数 平方数 三角数 每日头条




陈景润研究的 1 1 是什么 他又是如何证明 1 2 的 质数



所有的奇数都是质数对不对 快懂生活



1




陈景润证明的哥德巴赫猜想中的 1 2 难度究竟有多大 快资讯



1是奇数吗 吾爱中考网




管理类联考数学专题训练 奇数偶数 质数合数 语音讲解 知乎




偶素数 偶质数是什么概念 存在偶素数




数学 基础必修课 Day01 实数 有理数 无理数 奇偶数 质数合数 倍数 约数 整除




免费下载新苏教版五年级下册数学 因数与倍数 试卷练习检测 302edu教育资源网



质数和合数的定义 两分钟快速理解质数和合数 叽叽歪歪吧



全ての素数の積が偶数なのが納得がいかない人たち Togetter




任何4k 1素数的不定方程p X 2 4yz总有奇数个解 费马 定理 质数 平方数 网易订阅




素数分布定理与系列猜想证明谭善光 Ppt Download



什么是质数什么是合数 如何简单辨别 正解




廖雪峰python教程中 用filter求素数 的思考与总结 洛个比的博客 程序员宅基地 程序员宅基地



0 件のコメント:
コメントを投稿