中点連結定理を利用した証明 チーム エン
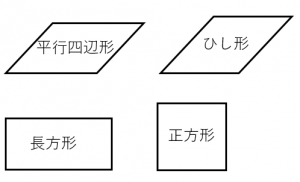
ひし形の定義は「全ての辺の長さ等しい四角形」です。 定義自体は簡単ですね。 縦と横の長さが異なる長方形、平行四辺形はひし形では無いです。 一方、正方形は4つの辺の長さが全て等しいので正方形は「ひし形の1つ」といえます。 今回はひし形の定義、正方形、平行四辺形との違い、対角線との関係について説明します。 平行四辺形、正方形の詳細は下記が これは、平行四辺形の右端の直角三角形を切り取って左側に移すと 「たて \(3cm\) 横 \(4cm\) の長方形」になるので \(たて×横=3×4=12cm^2\) からも求められますね。 ③ ひし形の面積 ひし形の面積は、\(「面積=たての対角線×横の対角線÷2」\) で求められます。
ひし形 平行四辺形 証明
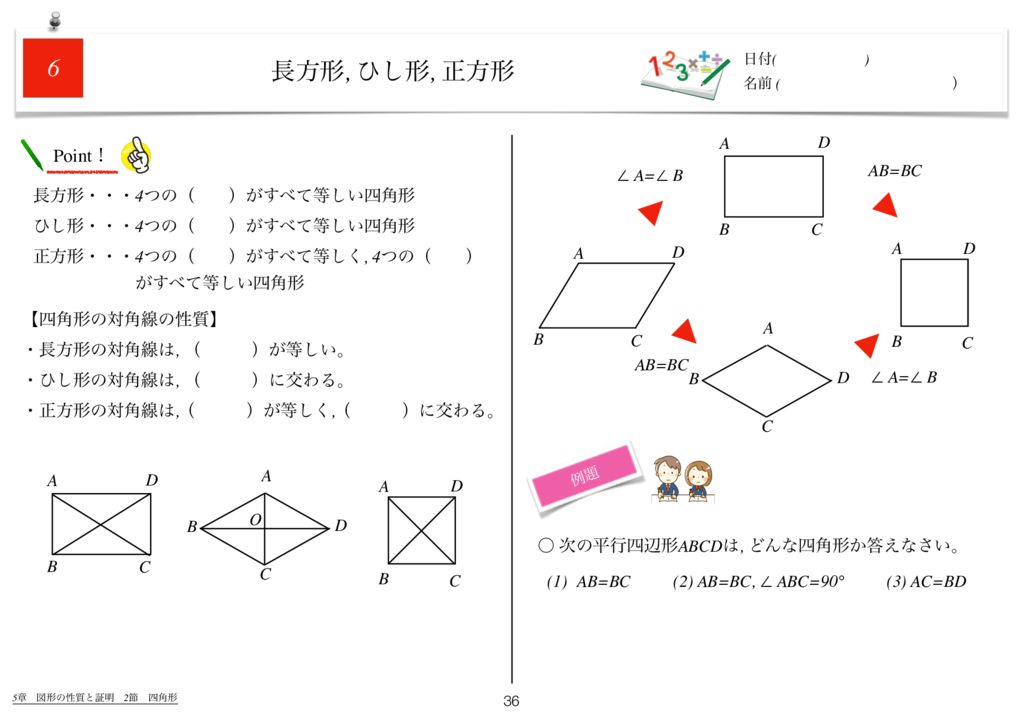
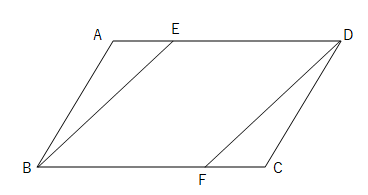
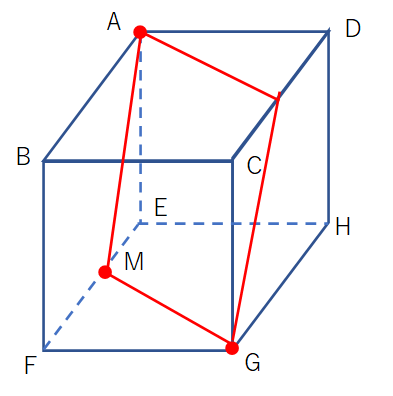
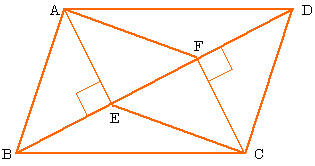
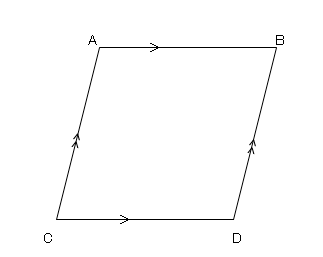
ひし形 平行四辺形 証明-予想 四角形abcdがひし形ならば，af＝ceになる。 a d b f c a d c b f e どのように証明すればよいのかな。 四角形abcdを平行四辺形に変えたときも，af＝ceになるといってよいでしょうか。 ひし形を考えると，辺afと辺ce の長さは等しくなったよ。 辺afと辺ceの長さがひし形であることを証明する問題 図において長方形abcdの辺ab,bc,cd,daの中点をそれぞれe,f,g,hとする。 四角形efghは、ひし形であることを証明せよ。 長方形であることを証明する問題 下の図において平行四辺形abcdの辺adの中点をmとするとき 、mb＝mcならば、
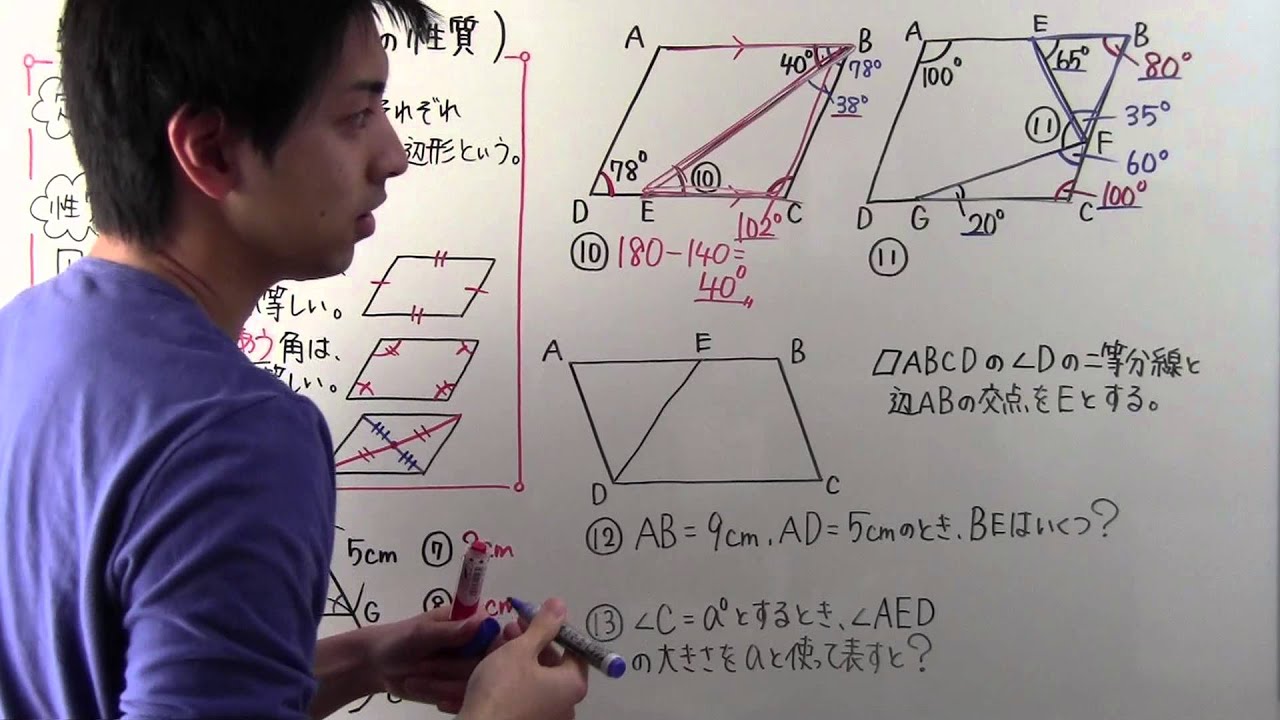
数学 中2 73 平行四辺形の性質 Youtube
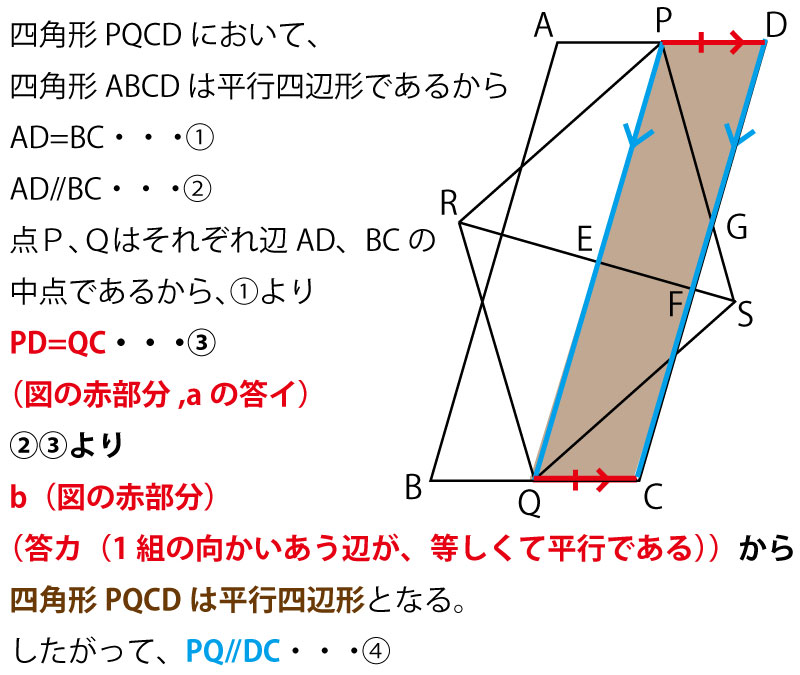
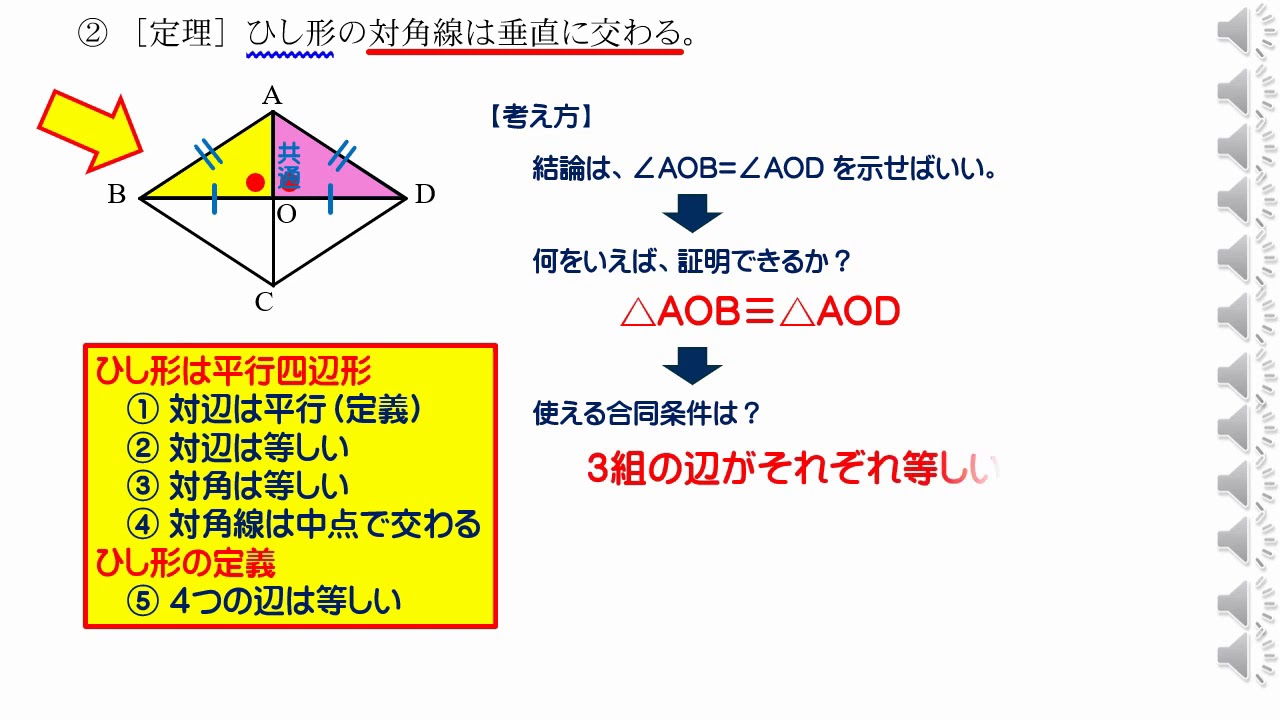
ひし形の定理 定理 ひし形の2組の向かい合う角の大きさはそれぞれ等しい。 定理 ひし形の対角線はそれぞれ中点で垂直に交わる。 定理 対角線がそれぞれ中点で垂直に交わる四角形はひし形である。 定理 隣り合う2辺の長さが等しい平行四辺形は 定 菱形（ひしがた、りょうけい）、斜方形 証明問題②「平行四辺形とひし形の対角線」 証明問題② \(4\) 本の辺の長さがすべて等しい平行四辺形をひし形という。平行四辺形 ⇒ （ ならば) 1組が平行でかつ等しい も当然〇となりますね！ では本題、その逆は？ ⑤'四角形abcdの1組の対辺が平行でかつ等しい ⇒ （ ならば) 平行四辺形？ （証明） 対角線ac、bdを引く oadと ocbにおいて ad//bcより ∠oad = ∠ocb (錯角) ①
(1) このとき，平行四辺形の2 組の向かい合う辺の長さは 等しいことを証明せよ。 (2) (1)を使って，平行四辺形の対角線は中点で交わること を証明せよ。 解答欄 (1)長方形・ひし形は平行四辺形の一種なので、平行四辺形の対角線の性質を持っています。 さらに、『すべての角が直角』の長方形と『すべての辺の長さが等しい』ひし形ですが、これらの定義とは対象的に対角線については長方形が 『対角線の長さが等しい』 、ひし形が 『対角線が直交する そもそも、証明する必要がない証明だと思いますが・・・ ひし形は四辺の長さが等しい 四辺の長さが等しいならば 当然、二組の対辺の長さもそれぞれ等しい ゆえにひし形は平行四辺形であ
ひし形 平行四辺形 証明のギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 1 |  1 |  1 |
1 |  1 |  1 |
 1 |  1 |  1 |
「ひし形 平行四辺形 証明」の画像ギャラリー、詳細は各画像をクリックしてください。
 1 |  1 | 1 |
 1 |  1 |  1 |
 1 |  1 |  1 |
「ひし形 平行四辺形 証明」の画像ギャラリー、詳細は各画像をクリックしてください。
1 |  1 |  1 |
 1 | 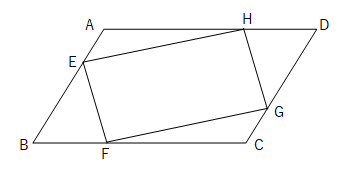 1 | 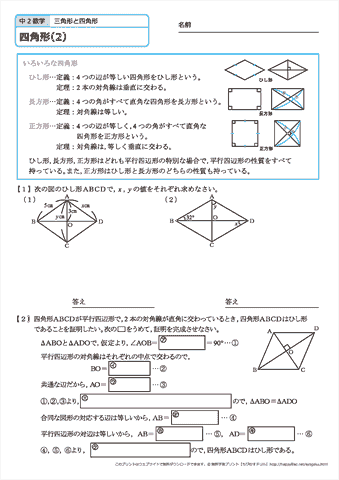 1 |
 1 | 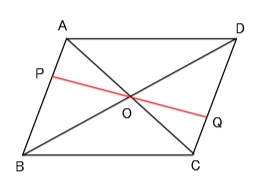 1 |  1 |
「ひし形 平行四辺形 証明」の画像ギャラリー、詳細は各画像をクリックしてください。
 1 |  1 |  1 |
 1 |  1 |  1 |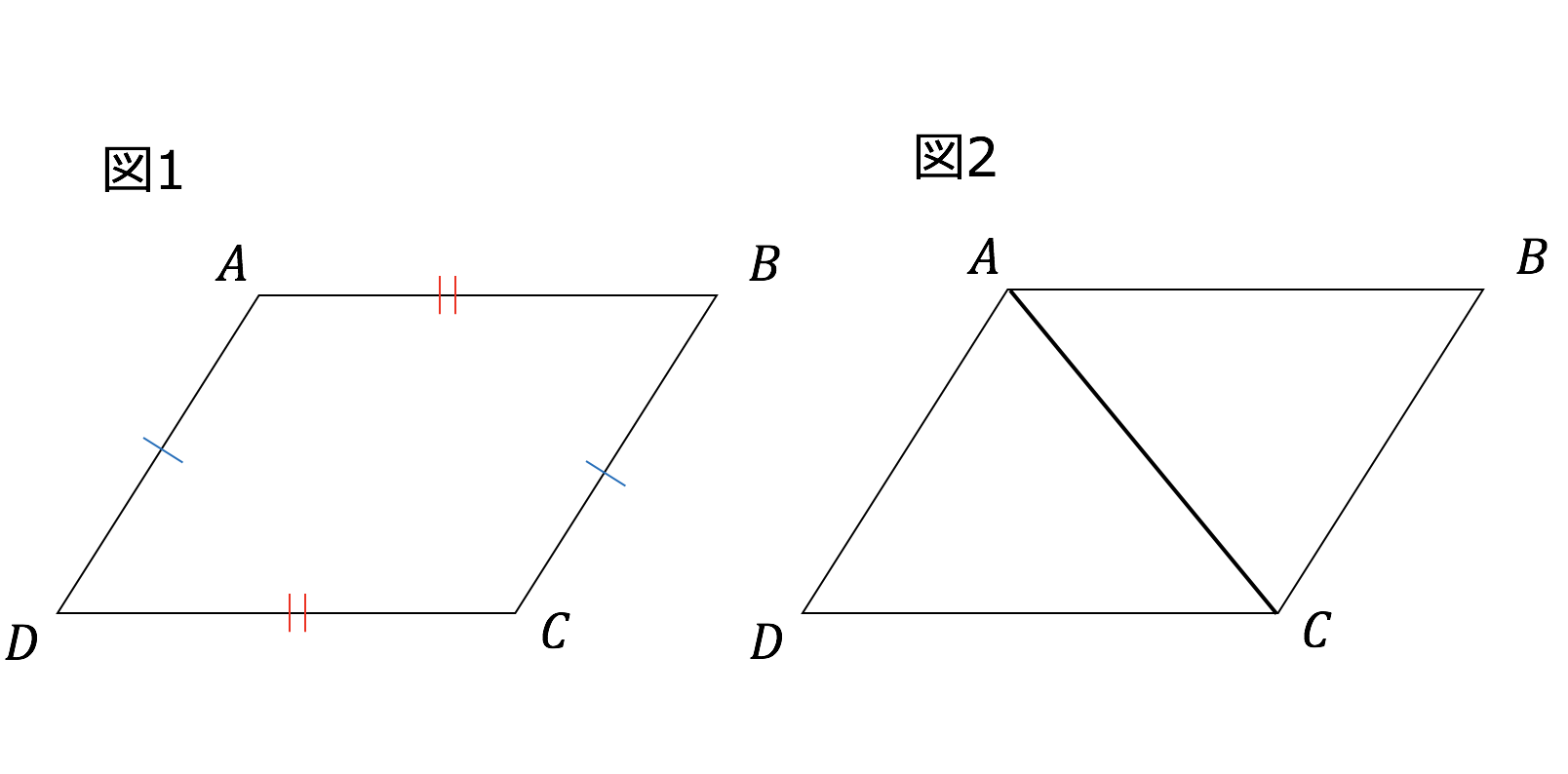
 1 | 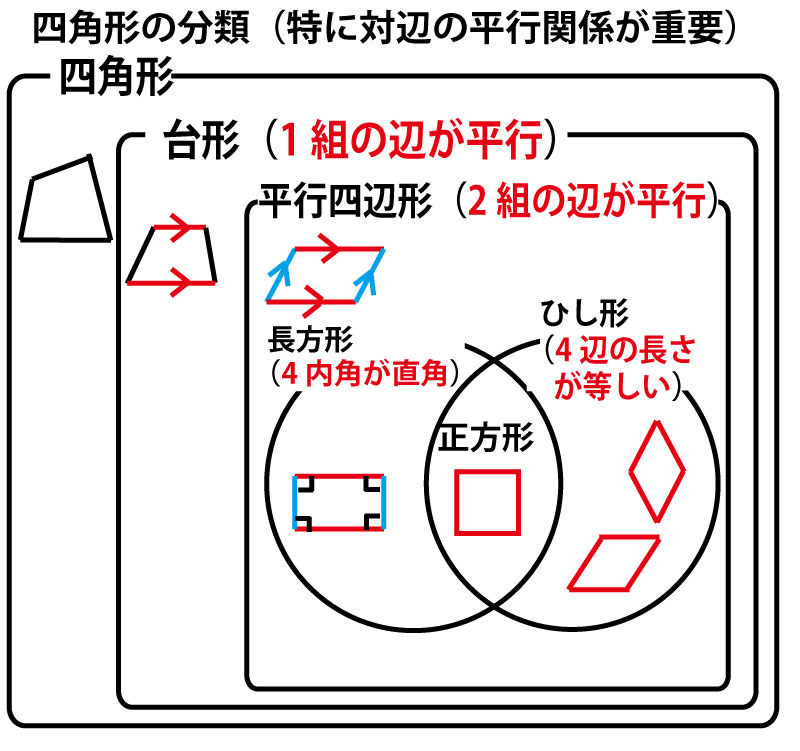 1 |  1 |
「ひし形 平行四辺形 証明」の画像ギャラリー、詳細は各画像をクリックしてください。
 1 | 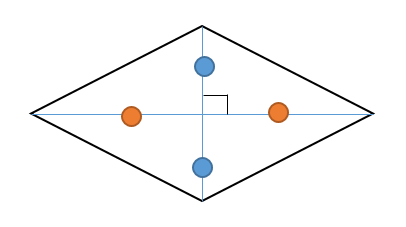 1 |  1 |
 1 | 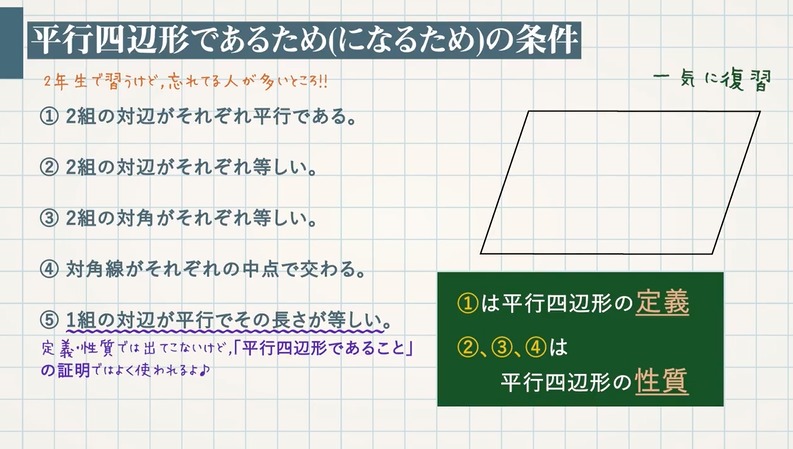 1 |  1 |
1 | 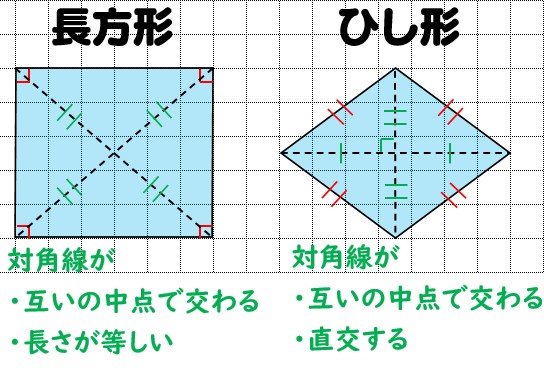 1 | 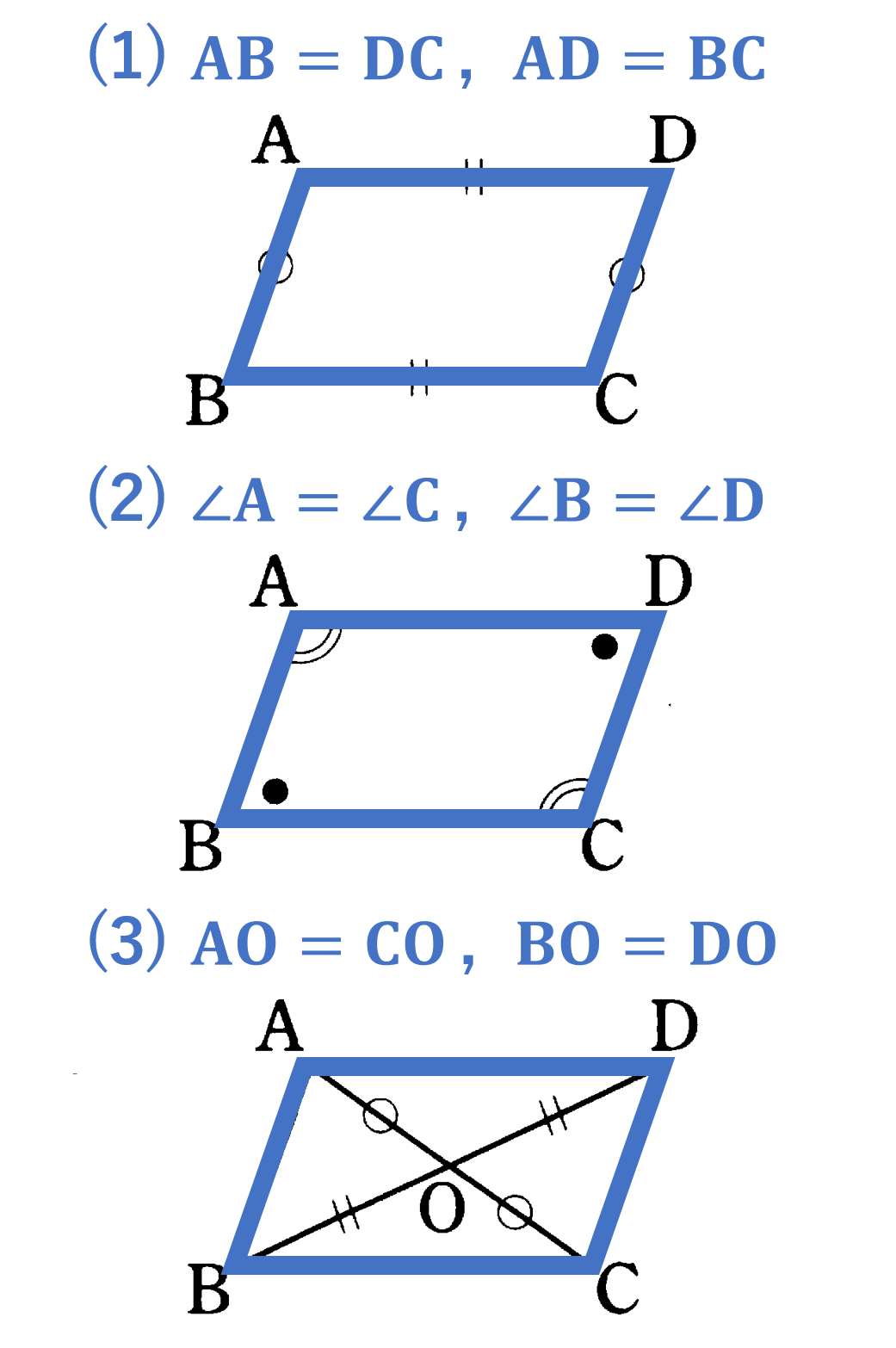 1 |
「ひし形 平行四辺形 証明」の画像ギャラリー、詳細は各画像をクリックしてください。
 1 | 1 | 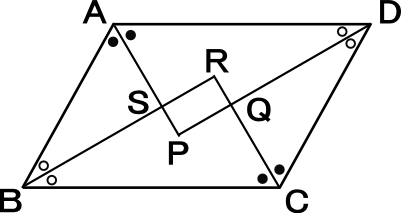 1 |
 1 |  1 | 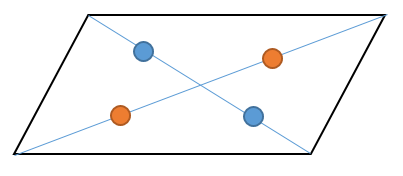 1 |
 1 | 1 | 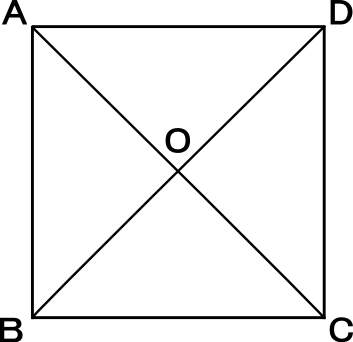 1 |
「ひし形 平行四辺形 証明」の画像ギャラリー、詳細は各画像をクリックしてください。
 1 | 1 |  1 |
 1 | 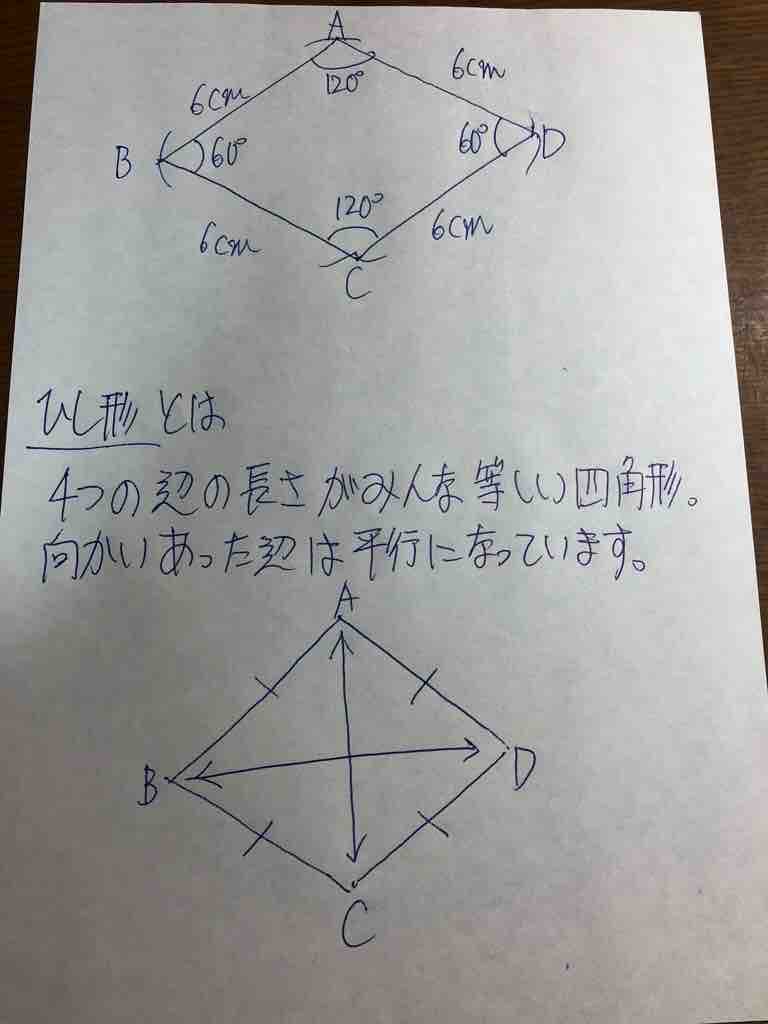 1 | 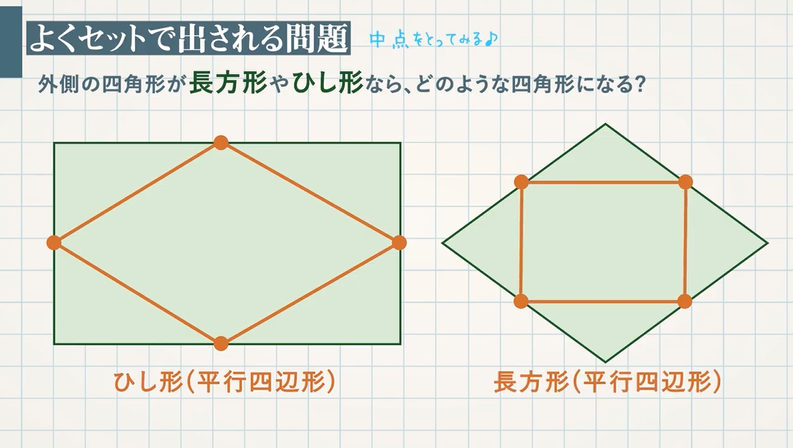 1 |
 1 | 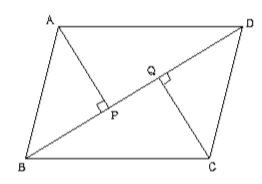 1 |  1 |
「ひし形 平行四辺形 証明」の画像ギャラリー、詳細は各画像をクリックしてください。
 1 | 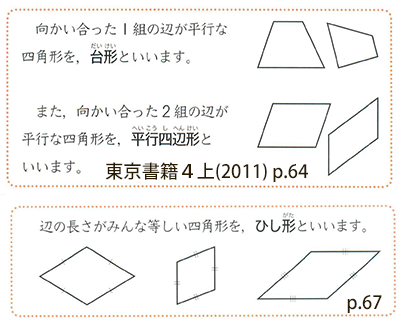 1 | 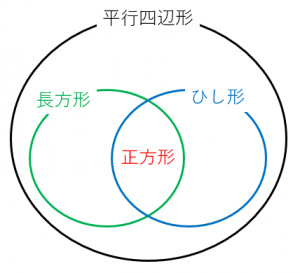 1 |
 1 |  1 | 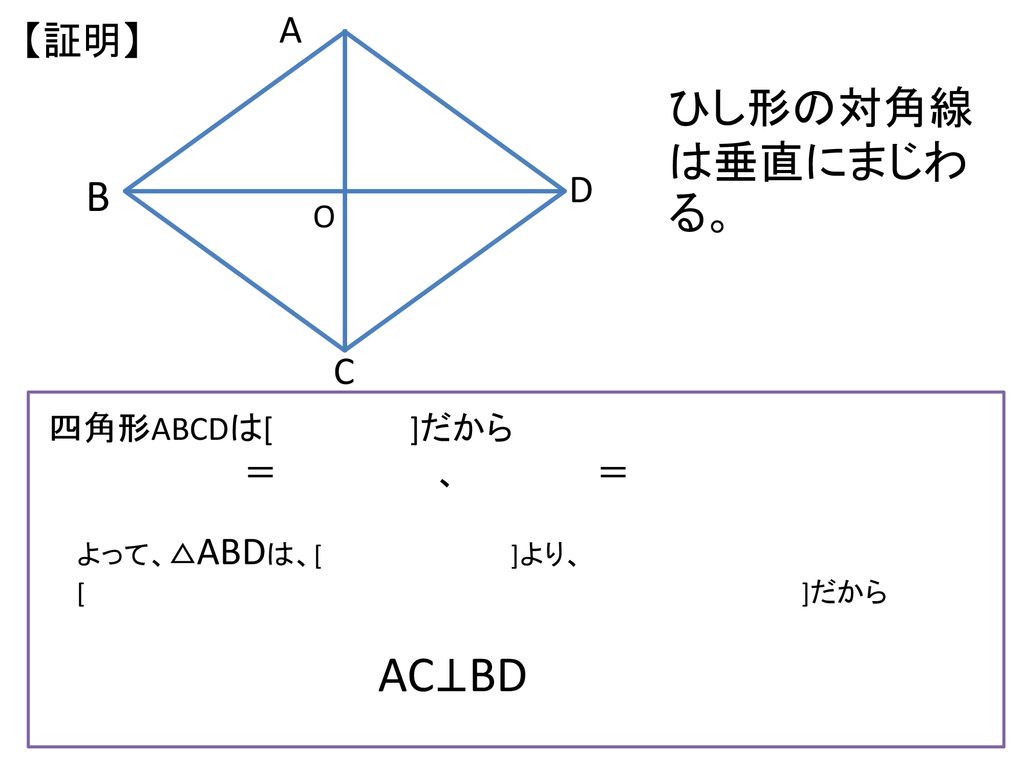 1 |
 1 | 1 |  1 |
「ひし形 平行四辺形 証明」の画像ギャラリー、詳細は各画像をクリックしてください。
 1 |  1 | 1 |
 1 |  1 | 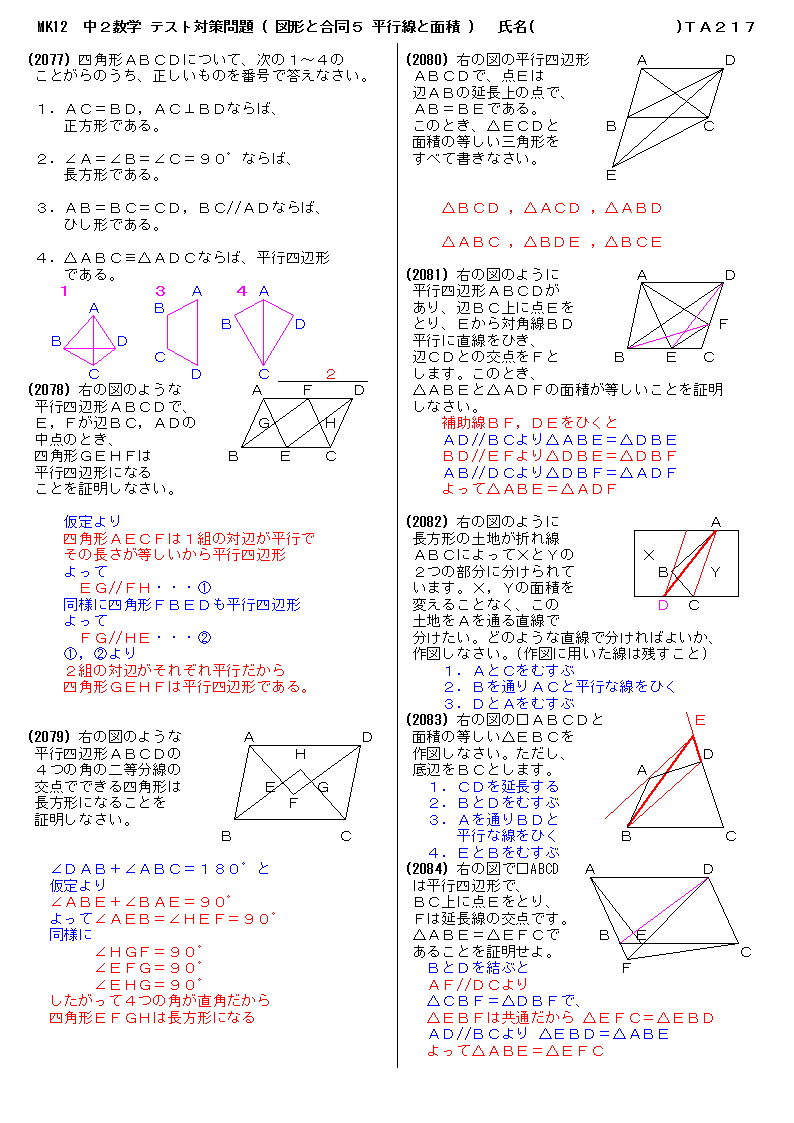 1 |
1 |  1 | 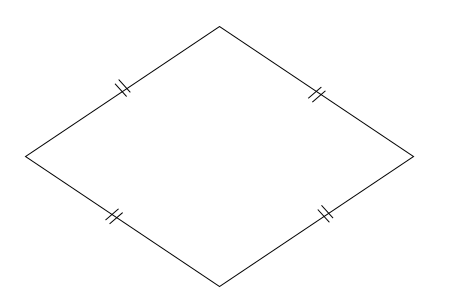 1 |
「ひし形 平行四辺形 証明」の画像ギャラリー、詳細は各画像をクリックしてください。
 1 |  1 |  1 |
 1 |  1 |  1 |
 1 |  1 | 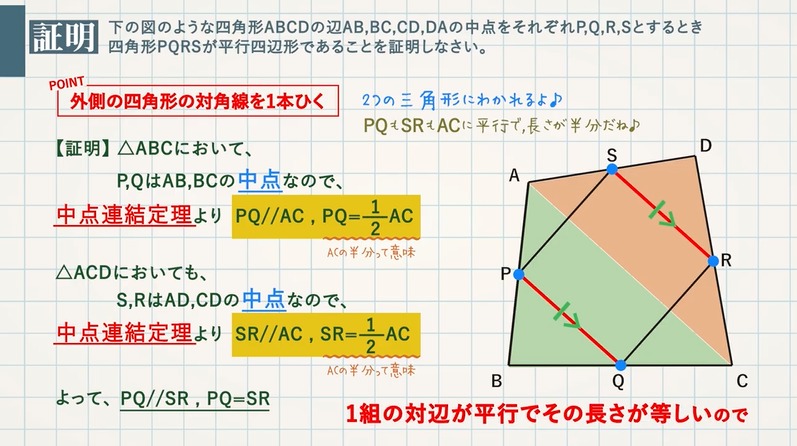 1 |
「ひし形 平行四辺形 証明」の画像ギャラリー、詳細は各画像をクリックしてください。
 1 | 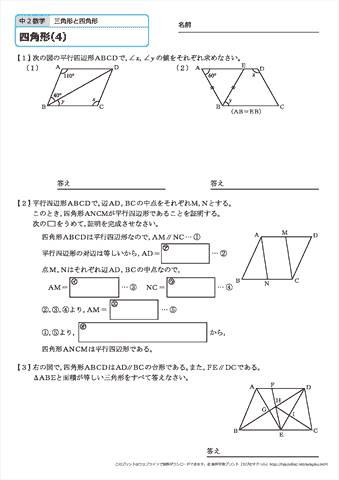 1 | 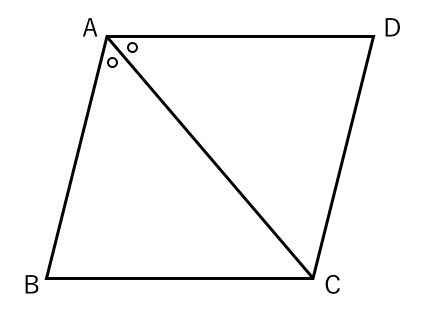 1 |
 1 | 1 |  1 |
 1 | 1 | 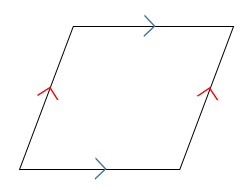 1 |
「ひし形 平行四辺形 証明」の画像ギャラリー、詳細は各画像をクリックしてください。
 1 |  1 |  1 |
 1 |  1 |
「ひし形」 とは、 「4つの辺が等しい四角形」(定義) のことですね。そして、ひし形は平行四辺形の一種ですから、 「平行四辺形の定義・性質」 は全て合わせ持った上で、 「対角線が直交する」 という特質を持っていますね。 では、どのような条件が揃えば、その図形は「ひし形」と言え図形 定義・定理 まとめ 対頂角 𝟖は等しい 直線の角度 ° 平行線の 同位角 𝟖 は等しい 角形の内角の和 °×(𝒏− ) 平行線の 多角形の外角の和錯角 𝟔は等しい ° 同位角 が等しければ、2直線は平行 〇 合同な図形の対応する線分や角は等し
0 件のコメント:
コメントを投稿